Page History: Capacitive Dropper Calculator for Current and Capacitance
Compare Page Revisions
Page Revision: 2020/06/04 17:22
Often times you need a small amount of power derived from a mains source - perhaps just a few tens of milli-amps to drive a micro-controller. In such cases, it can be difficult to justify the expense and size of a switched mode PSU let alone a transformer-based linear PSU. Very often, a resistor is used to reduce voltages to working levels, but with mains, there is a lot to "shave off" and resistors are quite inefficient for such an application. Simply "burning off" the excess, they generate a lot of heat which needs to be vented and this leads to large bulky resistors... back to square one.
A better way (with caveats - we will approach in a moment) is to use a
capacitive dropper circuit. It uses the phenomenon of capacitive reactance to pass only a portion of the available power, so they look a bit like a resistor to the supply but you get none of the downsides of actually using a resistor. When deriving power from mains in this manner the capacitor needs to be rated at 400V (Peak mains in UK can be 350V) and it should be "
X" rated.
A few years back I had a need to provide a great many lighting controllers that fitted inside a ceiling rose and controlled the light on the pendant below. A PSU module would have added considerably to the project cost ignoring the confines of the ceiling rose. A capacitive dropper was designed on the controller board, fitted perfectly in the space available and provided the 75mA required.
CaveatsBefore you rush off thinking capacitive droppers are a miracle answer to small mains powered PSUs, you should consider the following:
- a. It is vital to get the mains Live and Neutral connections the right ways round to avoid the very serious, possibly fatal, risk of electric shock. If reversed, your dropper will still work, but the 0V/GND rail will be at mains potential. If someone innocently touches or attaches something to 0V (which is usually fine) and then bridges to an earth connection - the full mains potential is now routed through them.
- b. There is no Galvanic isolation of the circuit. The 0V/GND rail is connected to the mains Neutral - this is not in itself an issue in a properly functioning mains electrical system (see above). Attaching any mains powered device to the DC side of such a circuit will probably trip the RCD at the consumer board. This is because a tiny amount of current will leak back to neutral through the device (instead of all the back-flow returning via the circuit's neutral connection). The RCD will see the imbalance of current on the circuit, think something bad is happening and trip the power to minimise any injury. To attach equipment on the DC side (e.g. an oscilloscope), it must be either, battery powered or it (or, preferably, your dropper) must be powered via an isolation transformer.
The calculation behind all this is fairly simple, based on the electrical principles staple for reactance of a capacitor;
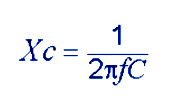
Below is a tiddly trinket (I used MMBasic but it is simple enough to transcribe into just about any language) to take the required values and quickly determine either the current you can get from a dropper circuit based on the value of its capacitor or the capacitance required to supply a given current. It isn't rocket-science but it takes the grunt out of one more chore.
Dim Float C,V,F,A
Dim y$
Print "***************************************************"
Print "* Capacitive dropper Current/Capacitor calculator *"
Print "***************************************************"
Do
Print: Print "Which do you wish to calculate:"
Print "The Current available in a circuit[A]"
Print "or"
Print "The Capacitance required to deliver a given current[C]"
Input y$
y$=Ucase$(y$)
Loop Until y$="A" or y$="C"
If y$="A" Then
Input "Enter Supply Voltage (Vrms): ",V
Input "Enter Supply Frequency (Hz): ",F
Input "Enter Capacitor Value (nF): ",C
c=c/1e9' coz nF
A=2*Pi*C*V*F*1000
Print "Available Current is : ";STR$(A, 7, 5);"mA"
Else
Input "Enter Supply Voltage (Vrms): ",V
Input "Enter Supply Frequency (Hz): ",F
Input "Enter Desired Current (mA): ",A
a=a/1e3' coz mA
C=(1/(2*Pi*V*F))*A*1e9
Print "Required Capacitance is : ";Str$(C,1,3);"nF"
EndIf
worked example:
> RUN
Which do you wish to calculate:
The Current available in a circuit [A]
or
The Capacitance required to deliver a given current [C]
? c
Enter Supply Voltage (Vrms): 240
Enter Supply Frequency (Hz): 50
Enter Desired Current (mA): 50
Required Capacitance is : 663.146nF
>
This is good. A 0.68uF 400V X type capacitor will deliver the required current of 50mA.