For the past few decades, there has been a move to specific temperature sensing ICs, Some direct contact others using thermocouples etc.
These all require interfacing using some communication bus (I2C, SPI, OneWire etc...) with a degree of configuration, reading registers within the device when a measurement is required. Largely these provide an excellent method with good precision and all the hassle of stabilization taken away by the manufacturer in the design of the chip.
In recent years, the spectre of far-eastern counterfeiting and copying of electronic components has risen to a crescendo and had a "poisoning" effect on supply with even reputable suppliers being duped into providing second rate or even fake components that serve no purpose other than relieving you of your cash. It can be exceptionally difficult to secure genuine parts with much testing required from multiple sources to ensure a reliable component. Getting such fakes to work can be a major headache and waste of time.
This has driven me to explore an older method for temperature measurement, achieved using a highly temperature variable resistor called a
Thermistor - all components experience some variability due to heating, but thermistors are manufactured from materials that are particularly "badly" affected - deliberately. In this article all references to thermistor assume a Negative Temperature Co-efficient part (NTC) - i.e. the resistance varies in the opposite direction (negatively proportional) to the temperature... as the temperature rises, the resistance falls and vice versa.
It is important to note that thermistors are not linear devices - that is a temperature change of one degree may have a larger impact on resistance at one end of its range than at the other - the response follows a logarithmic curve. Measurement of temperature using a thermistor needs a small amount of mathematics to render a reliable reading. Values are remarkably consistent and when taking into account two key properties of thermistors, quite accurate.
Firstly, most thermistors have a resistance rating given at a specific temperature - this is most usually measured at 25 degrees Celsius - the R25 value (actually all the following equations use Kelvin but the R25 value is for human consumption - we'll adjust for that).
Secondly, a component design value, Beta (β or simply B - a derivative from the Steinhart–Hart equation) describes the characteristics of the logarithmic response.
Armed with R25, Beta and the supply voltage, we can calculate a surprisingly accurate temperature by measuring the voltage at the junction of the thermistor and a "balancing" resistor as shown below (the supply voltage is arbitrary).
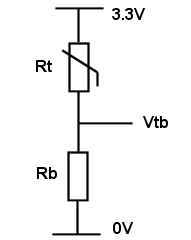
Much of the following code was inspired by a very good article
here:
The thermistor used was a ceramic bead NTC with the following properties:
R25=10K
Beta=3950
The code that follows is written in MMBasic and from testing on a 28pin MicroMite, please tweak as necessary. It is largely commented/self-explanatory. A derivation of this is used to sense the temperature of the heated build plate on my 3D printer.
Do remember the temperature is as measured at the thermistor body. Any differences in distance and contact with the desired item will vary. On my heated bed, the temperature above the heaters is around 10C higher, but right over the sensor is +/- 2C - perfectly acceptable for the application.
The Code:
Const Beta=3950
Const Tct=25+273.15,Rct=10000' 25C in Kelvin - this is the calibration point of the thermistor i.e. 10K @ 25C. Change as necessary
Const Rb=1000'balance resistor
'Varying the balance resistor (Rb) moves the temperature range on the logarithmic parabola.
'Adjust so your delta (area with most pronounced change in voltage) is where it's best for you
'e.g. middle of the voltage range, AIN=1.65V,
'Rb 1K=83C, 2K2=59C, 4K7=39C
'for me, 1K gives 2.5V at 124`C which is just over the top of the desired range (60-120C) - ideal
Const Vcc=3.29' measure your supply voltage precisely for this value
Dim Float Vtb,Rt,Tc
SetPin 5,AIN
Do
Vtb=Pin(5)'voltage at junction of Rt and Rb
Rt=Rb*((Vcc/Vtb)-1)' calculate the resistance of the thermistor
Print "Rt resistance in Ohms",Rt,
Tc=((Beta*Tct)/(Beta+(Tct*Log(Rt/Rct))))-273.15 'calculate the temperature
Print"=";Tc;"`C"
Print
Pause 500' slow the loop a bit
Loop